No.032 袖のパターンメーキング（基本ロジック）

アパレル工業新聞　2022年3月1日発行 7面
この記事・写真等は、アパレル工業新聞社の許諾を得て掲載しています。

今回は袖がテーマです。袖は、パターンの中で最も悩ましく、最もパタンナーの技量が問われるパーツだと誰もが思っているでしょう。私も袖のパターンに関しては今もなお自信が持てないでいます。というのも、これは私の持論ですが、「どんなアームホールにも付く最適な袖山の形状を決めるロジックは存在しない」と思っているからです。そう、今まで経験だけで引いてきたわけです。そして引く度に何か納得できない自分がいるから厄介です。まさに永遠のテーマなのですね。 そんなこともあり、今回は自分自身で勉強をし直すつもりでこのテーマを採り上げることにしました。袖の基本を私なりのロジックで分析し、いろいろな袖のパターンメーキングを改めて実践してみたいと思います。まずは袖とは何ぞや？から始めますので、どうぞ一緒に袖の基本から考察しましょう。

１．まずは単純に、アームホールが円だとしたら？

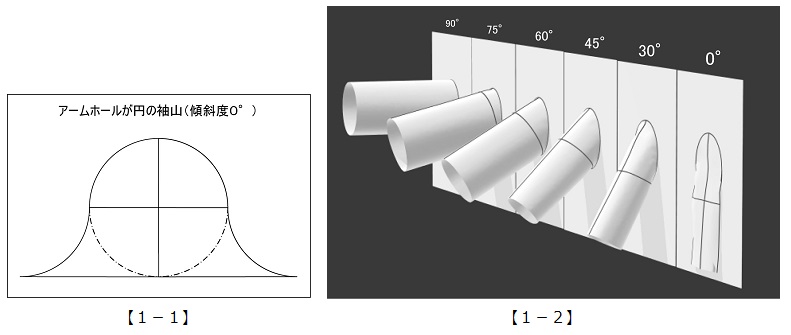
【１－１】円のアームホールに付く、袖山の高さが最大のときの袖山の形状。（イセ分は考慮しない。）当然、これでは腕が入らないので袖とは言えない。これを傾斜度0°の袖とする。

【１－２】袖の傾斜角度を比較した３Ｄ画像。袖に傾斜をつけることで腕が入る袖となる。角度が上がるほど袖が太くなり、最大ではアームホールと同一になる。

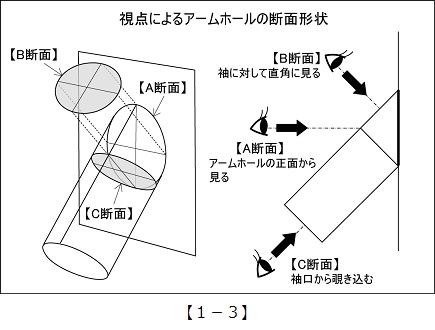
【１－３】袖に傾斜が付くと、袖山の高さと袖幅が変化する。それを求めるために、それぞれの傾斜に合わせた視点によるアームホールの断面形状が必要になる。アームホールを正面から見た形状をＡ断面（つまりアームホール形状のこと）、袖の傾斜に対して直角方向に見た形状をＢ断面、袖口から覗き込んで見た形状をＣ断面とする。

【１－４】傾斜度45°を例にした各視点からの袖の３Ｄ画像。

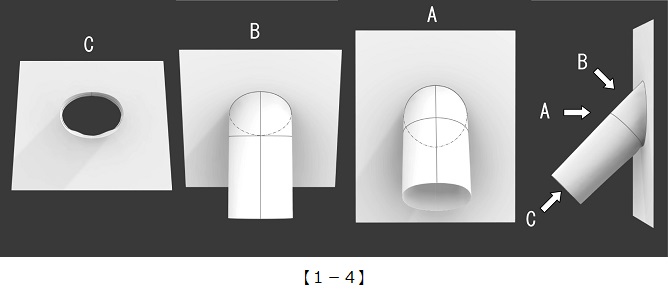
【１－５】傾斜度45°のＢ断面とＣ断面を求める式。この場合は三角関数を使用しているが、小難しい計算が嫌ならＣＡＤで楕円を引いて実寸法を測ってしまえばよい。この場合は45°のためＢ断面とＣ断面は同一形状になる。

【１－６】傾斜度45°の袖山の形状。Ｂ断面は袖山のカーブを引く際のガイドになり、Ｃ断面は袖幅を求めるときに必要となる。袖幅はＣ断面の円周だが、楕円の円周を求める式は非常に難しいので、短径と長径の値が分ればＣＡＤで楕円を引いて円周を測ってしまうほうが手っ取り早い。

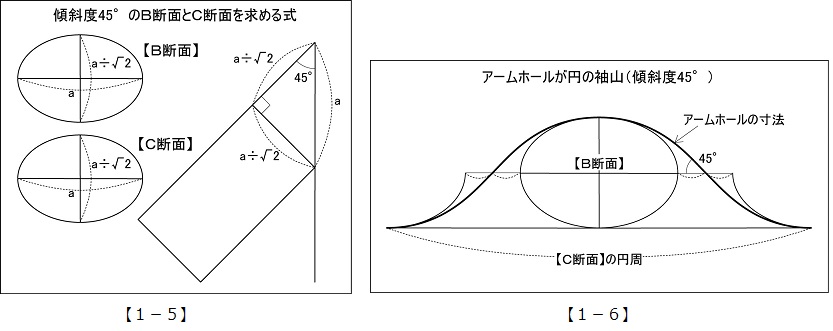
【１－７】傾斜度による袖山の変化を表した図。各袖幅の端点を結ぶと、ある一点を中心に弧を描く。

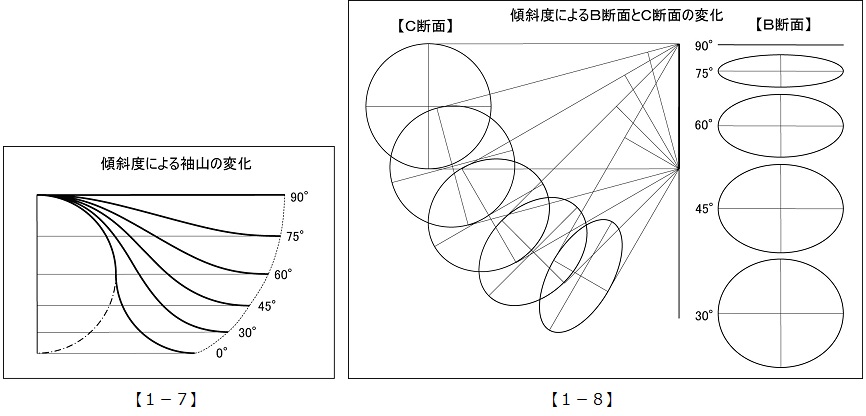
【１－８】傾斜度によるＢ断面とＣ断面の変化を表した図。Ｂ断面もＣ断面も長径は円の直径に等しく常に一定である。また、袖幅は最大で円周（アームホール寸法）と同じであり、それ以上になることはない。

２．アームホールを楕円にした場合

実際のアームホールに近づけるために、アームホールを楕円にして袖を引いてみる。ロジックは円の場合とまったく同じだが、各寸法は計算で求めるのが非常に面倒なのでＣＡＤで引いて実寸を測っている。

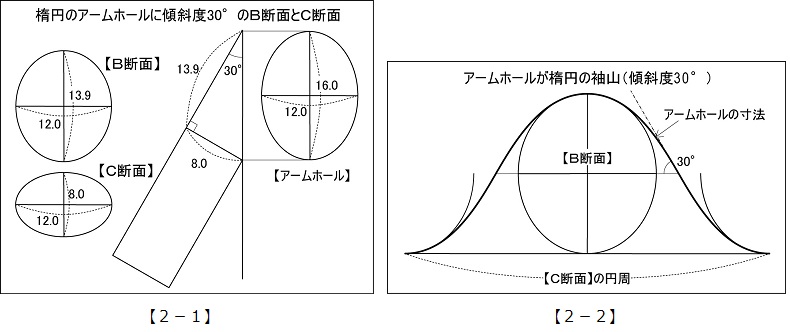
【２－１】楕円の長径（アームホール丈）と短径（カマ幅）はジャケットのアームホールを想定して設定している。袖の傾斜を30°とし、Ｂ断面とＣ断面を求める。

【２－２】各断面を基にして作図した傾斜度30°の袖山。

３．袖山にイセを入れた場合

【３－１】アームホールの最下点を基点に、袖を立てるように回転して傾斜度を少なくする。このとき袖山とアームホールとの間に出来る空隙が、袖山に上腕を包み込む容積を与える。

【３－２】空隙部分を袖山の上に積み足した状態の図。袖山の周長が長くなった分がイセになる。

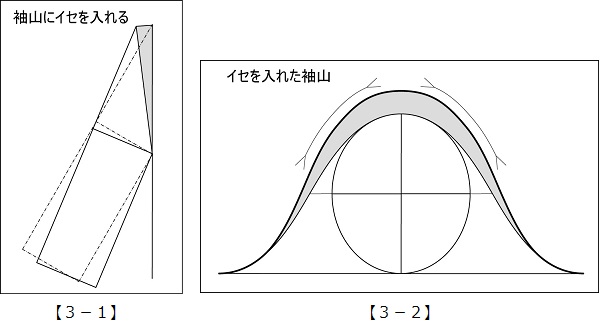
【３－３】傾斜度30°の袖にイセを入れた３Ｄ画像。

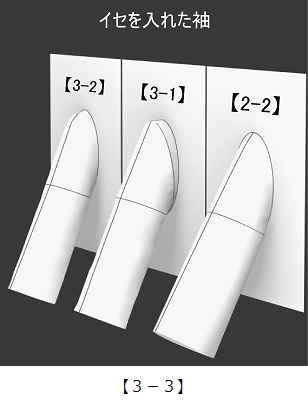
４．デッサンから袖山を作った場合

【４－１】実際のアームホールを基に、そこに付く袖の側面をデッサンで描く。

【４－２】アームホールと袖山の間に展開線を入れて反転する。隙間が空いた分がイセになる。イセの配分は袖に厚みを与えるために調整する。

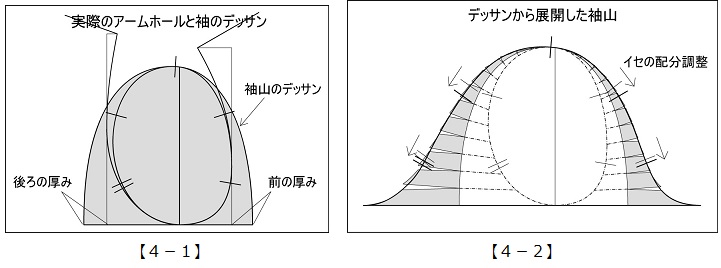
【４－３】デッサンから作った袖の３Ｄ画像。一応、袖らしくなっているが、デッサンの描き方は経験と感覚に頼るしかない。

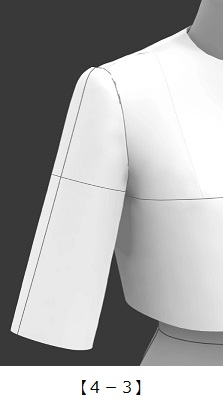
５．結局、袖とは？

袖の基本的な構造を理解するために、円や楕円など出来るだけ単純な図形を用いたロジックで解説をしたが、そもそもパターンメーキングは幾何学ではない。実際のアームホールは楕円ではないし平面でもない。複雑な曲面の上に不規則な曲線で形成されている。そこに付く袖山は当然複雑な形状になるであろうし、更に機能性と審美性を考慮して初めて衣服の一部となり得るのだ。自己矛盾になるが、前述したようにどんなアームホールにも付く最適な袖山の形状を決めるロジックは存在しないと思っている。今回考察をしてみて、やはりこの持論に戻ってしまうようだ。